题目
Bear and Two Paths
描述
熊岛有n个城市,编号为1到n。城市通过双向道路连接。每条路都连接着两个不同的城市。没有两条路是连接同一对城市的。
有一次,熊利马克在一个城市a,他想去一个城市b,但没有直接的连接,所以他决定走很长的路,每个城市正好走一次。从形式上看。
a和b之间没有路。
存在一个由n个不同的城市组成的序列(路径)v1,v2,…,vn,v1=a,vn=b,并且在vi和vi+1之间有一条路,为 。
有一天,类似的事情发生了。利马克想在一个城市c和一个城市d之间旅行。它们之间没有路,但存在一个n个不同城市的序列u1,u2,…,un,u1=c,un=d,并且在ui和ui+1之间有一条路。
此外,Limak认为在Bearland最多有k条路。他想知道自己的记忆是否正确。
给定n,k和四个不同的城市a,b,c,d,你能找到满足所有给定条件的可能路径(v1,…,vn)和(u1,…,un)吗?找到任何解决方案,如果不可能,则打印-1。
输入
输入的第一行包含两个整数n和k(4≤n≤1000,n-1≤k≤2n-2)–分别为城市的数量和允许的最大道路数量。
第二行包含四个不同的整数a、b、c和d(1≤a、b、c、d≤n)。
输出
如果不可能满足所有给定条件,则打印-1。否则,打印两行路径描述。这两行中的第一行应该包含n个不同的整数v1,v2,…,vn,其中v1=a和vn=b。第二行应该包含n个不同的整数u1,u2,…,un,其中u1=c,un=d。
两条路径最多产生2n-2条路。(v1,v2), (v2,v3), …, (vn-1,vn), (u1,u2), (u2,u3), …, (un-1,un)。如果你的答案包含超过k条不同的道路或有任何其他条件的破坏,你的答案将被视为错误。请注意,(x,y)和(y,x)是同一条路。
样例
输入
7 11
2 4 7 3
输出
2 7 1 5 6 3 4
7 2 1 5 6 4 3
输入
1000 999
10 20 30 40
输出
-1
提示
在第一个样本测试中,应该有7个城市和最多11条道路。所提供的样本解决方案生成了10条道路,如图所示。你还可以看到长度为n的2到4的简单路径,以及7到3的路径。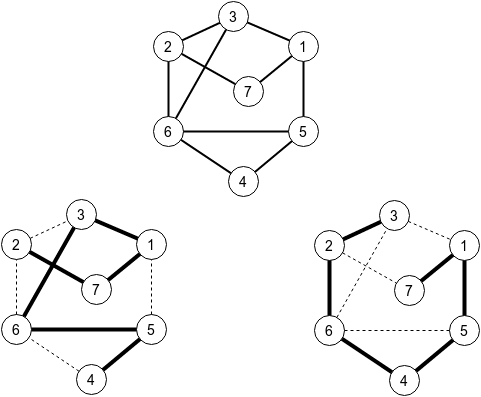
补充
时间限制 2 秒
内存限制 256 MB
来源 FYOJ
题解
按题目模拟即可~
就很奇怪
样例都通不过
交上去就AC了?
1 |
|
测评结果 通过
分数 100
时间 1 MS
内存 736 KB
语言 C++
代码长度 621
